Elektro- och informationsteknik

Lunds Tekniska Högskola | Lunds universitet

Projektbeskrivning

Physical bounds in antenna theory

2003-01-01 -> 2008-12-31

Projektbeskrivning

In this project, we analyze physical bounds (physical limitations) on antennas, ie we investigate questions as:

How do size and geometry affect the performance of an antenna?

or

What characterizes the best antenna that can be built within a given geometry?

Our approach (see also research)

  1. Uses an identity (sum rule) that relates the extinction cross section of a scatterer with the polarizability of the object.
  2. The effective antenna aperture (equals the absorption cross section for lossless antennas) is bounded by the extinction cross section.
  3. Rewrite as an antenna identity that relates the realized gain with the polarizability.
  4. Use that the polarizability is monotonic to express the result in an arbitrary circumscribing geometry.
  5. Estimate the integral to obtain the final bounds.

Results

  • The new bounds are valid for arbitrary circumscribing geometries.
  • They resemble the Chu (and Thal) bound for spherical geometries.
  • They separate electric and magnetic material properties.
  • They provide a dependence of the polarization.

physical bounds for planar antennasphysical limitations cylindrical antennas

  1. M. Gustafsson, C. Sohl, G. Kristensson:
    Physical limitations on antennas of arbitrary shape
    Proc. Roy. Soc. A, Vol. 463, No. 2086, pp. 2589-2607, 2007. TEAT-7153
  2. C. Sohl, M. Gustafsson:
    A priori estimates on the partial realized gain of ultra-wideband (UWB) antennas
    Quart. J. Mech. Appl. Math.,Vol. 61,No. 3, pp. 415-430, 2008. TEAT-7160
  3. M. Gustafsson, C. Sohl, G. Kristensson:
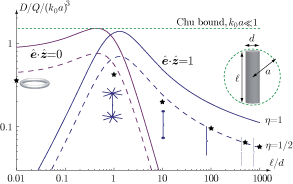
    Illustrations of new physical bounds on linearly polarized antennas
    IEEE Trans. Antennas Propagat.,Vol. 57,No. 5, pp. 1319-1327, 2009.
  4. A. Derneryd, M. Gustafsson, G. Kristensson, C. Sohl:
    Application of gain-bandwidth bounds on loaded dipole antennas
  5. M. Gustafsson, C. Sohl:
    New physical bounds on elliptically polarized antennas
    European Conference on Antennas and Propagation, Berlin, Germany, pp. 1-3, 2009-03-23.

Background

The investigations of this problem go back to Wheeler (1947) and Chu (1948). Some references are given below. Note that the list isn't complete.

  • H.A. Wheeler 1947, 1959, 1975: Lumped element models.
  • L.J. Chu, 1948:
    • Computes a lower bound of the antenna radiation Q and an upper bound on D/Q.
    • Circumscribe the antenna with a sphere (radius a) and expand the EM-field in partial waves.
    • Use recurence relations for the partial waves and a circuit representation to determine the stored energy and the radiated power.
    • The results are Q1≥1/(ka)3+1/ka and D/Q≤3/2Q1, where k denotes the resonance wavenumber.
    • Chu also discusses the possibility to use Fano's bounds on broadband matching and he gives an approximate formula for Qn for higher order modes.
  • The approach by Chu have been extended in several steps, eg
    • R.F. Harrington, 1958, 1960, 1961; bounds on G and D. Disuss the combination of TE and TM modes, has a typo in the problem.
    • R.E. Collin and S. Rothschild, 1964: closed form expressions for Qn for n=1,2,.. and extend the analyze to cylinder waves.
    • R.L. Fante 1969, 1992: Q, D/Q, G/Q for combinations of TE and TM modes
    • J.S. McLean 1996: Q1 using explicit formulas for the modes and combined TE and TM modes.
    • J.C-E. Sten etal 2001: Q for antennas close to a conducting plane.
    • W. Geyi 2003: Q and G/Q for combined TE and TM modes.
    • A. Karlsson 2004: Q and G for antennas in a lossy medium.
    • D.H. Kwon 2005: G and Q for combined TE and TM modes.
    • H.L. Thal 2006: Excludes the interiour of the sphere.  
  • Some extensions of the bounds to spheroidals are reported.
    • H.D. Foltz and J.S. McLean 1999:
    • J.C-E. Sten etal 2001:
  • Relationships between radiation Q and bandwidth are eg discussed by
    • W. Geyi etal 2000:
    • A.D. Yaghjian and S.R. Best 2005:
    • A. Hujanen etal 2005:
    • M. Gustafsson and S. Nordebo 2006, 2007:
    • R.C. Hansen 2006, 2008:
    • H. Stuart etal. 2007:
  • The bounds for combined TE and TM modes are criticized in
    • Grimes etal 1995, 1997, 2000 (see also Collin 1998)
References
  1. H. A. Wheeler,  Fundamental limitations of small antennas,  Proc. IRE, vol. 35, no. 12, pp. 1479-1484, 1947.
  2. L. J. Chu,  Physical limitations of omni-directional antennas,  Appl. Phys., vol. 19, pp. 1163-1175, 1948.
  3. R. Harrington, On the gain and beamwidth of directional antennas," IEEE Trans. Antennas Propagat., vol. 6, no. 3, pp. 219-225, 1958.
  4. H. Wheeler, The radiansphere around a small antenna, Proceedings of the IRE, vol. 47, no. 8, pp. 1325-1331, 1959.
  5. R. F. Harrington,  Effect of antenna size on gain, bandwidth and effciency,  Journal of Research of the National Bureau of Standards - D. Radio Propagation, vol. 64D, pp. 1-12, January - February 1960.
  6. R. F. Harrington, Time Harmonic Electromagnetic Fields. New York: McGraw-Hill, 1961.
    R. E. Collin and S. Rothschild,  Evaluation of antenna Q,  IEEE Trans. Antennas Propagat., vol. 12, pp. 23-27, Jan. 1964.
  7. R. L. Fante,  Quality factor of general antennas,  IEEE Trans. Antennas Propagat., vol. 17, no. 2, pp. 151-155, Mar. 1969.
  8. R. C. Hansen, Fundamental limitations in antennas," Proc. IEEE, vol. 69, no. 2, pp. 170-182, 1981.
  9. D. Grimes and C. Grimes, Bandwidth and Q of antennas radiating TE and TM modes, IEEE Trans. Electromagn. Compatibility, vol. 37, no. 2, pp. 217-226, 1995.
  10. J. S. McLean,  A re-examination of the fundamental limits on the radiation Q of electrically small antennas,  IEEE Trans. Antennas Propagat., vol. 44, no. 5, pp. 672-676, May 1996.
  11. D. Grimes and C. Grimes, Minimum Q of electrically small antennas: A critical review, Electron Lett, vol. 33, no. 433, p. 434, 1997.
  12. R. E. Collin,  Minimum Q of small antennas,  J. Electro. Waves Applic., vol. 12, pp. 1369-1393, 1998.
  13. W. Geyi, P. Jarmuszewski, and Y. Qi, The Foster reactance theorem for antennas and radiation Q,  IEEE Trans. Antennas Propagat., vol. 48, no. 3, pp. 401-408, Mar. 2000.
  14. C. Grimes, G. Liu, D. Grimes, and K. Ong, Characterization of a wideband, low-Q, electrically small antenna, Microwave and Optical Technology Letters, vol. 27, no. 1, pp. 53-58, 2000.
  15. J. C.-E. Sten, P. K. Koivisto, and A. Hujanen, Limitations for the radiation Q of a small antenna enclosed in a spheroidal volume: axial polarisation,  AEÜ Int. J. Electron. Commun., vol. 55, no. 3, pp. 198-204, 2001.
  16. W. Geyi, Physical limitations of antenna," IEEE Trans. Antennas Propagat., vol. 51, no. 8, pp. 2116-2123, Aug. 2003.
  17. A. Karlsson, Physical limitations of antennas in a lossy medium,  IEEE Trans. Antennas Propagat., vol. 52, pp. 2027-2033, 2004.
  18. A. D. Yaghjian and S. R. Best, Impedance, bandwidth, and Q of antennas,  IEEE Trans. Antennas Propagat., vol. 53, no. 4, pp. 1298-1324, 2005.
  19. R. C. Hansen, Electrically small, superdirective, and superconductive antennas. New Jersey: John Wiley & Sons, 2006.
  20. M. Gustafsson and S. Nordebo, Bandwidth, Q factor, and resonance models of antennas, Progress in Electromagnetics Research, vol. 62, pp. 1-20, 2006.
  21. H. L. Thal, New radiation Q limits for spherical wire antennas," IEEE Trans. Antennas Propagat., vol. 54, no. 10, pp. 2757-2763, Oct. 2006.
  22. M. Gustafsson and S. Nordebo, On the spectral effciency of a sphere, Progress in Electromagnetics Research, vol. 67, pp. 275-296, 2007.
  23. H. Stuart, S. Best, and A. Yaghjian, Limitations in relating quality factor to bandwidth in a double resonance small antenna, Antennas and Wireless Propagation Letters, vol. 6, 2007.
  24. R.C. Hansen, Bode and Fano impedance matching, Microwave and Optical Technology Letters, vol. 50, no. 4, pp. 875-877, 2008.
Sidansvarig: |